data-structure-typed/README_zh-CN.md

data-structure-typed

English | 简体中文

为什么

JavaScript和TypeScript的数据结构。

是否羡慕C++ STL (std::)、Python的 collections 和Java的 java.util？

不再需要羡慕了！JavaScript和TypeScript现在拥有 data-structure-typed。

基准测试 与C++ STL相比。API 标准 与ES6和Java对齐。易用性 可与Python媲美。

提供了JS/TS中没有的数据结构

Heap, Binary Tree, RedBlack Tree, Linked List, Deque, Trie, Directed Graph, Undirected Graph, BST, AVL Tree, Priority Queue, Queue, Tree Multiset.

性能超越原生JS/TS

方法名	耗时（毫秒）	数据规模	所属标准库
Queue.push & shift	5.83	100,000	data-structure-typed
Array.push & shift	2829.59	100,000	原生JS
Deque.unshift & shift	2.44	100,000	data-structure-typed
Array.unshift & shift	4750.37	100,000	原生JS
HashMap.set	122.51	1,000,000	data-structure-typed
Map.set	223.80	1,000,000	原生JS
Set.add	185.06	1,000,000	原生JS

安装和使用

现在你可以在 Node.js 和浏览器环境中使用它

CommonJS：require export.modules =

ESModule：   import export

Typescript：   import export

UMD：           var Deque = dataStructureTyped.Deque

npm

npm i data-structure-typed --save

yarn

yarn add data-structure-typed

import {
  BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
  AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultiMap,
  DirectedVertex, AVLTreeNode
} from 'data-structure-typed';

CDN

将下面的代码复制到 HTML 文档的头标签中。

开发环境

<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.js'></script>

生产环境

<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.min.js'></script>

将下面的代码复制到你的 HTML 的 script 标签中，你就可以开始你的开发了。

const {Heap} = dataStructureTyped;
const {
  BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
  AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultiMap,
  DirectedVertex, AVLTreeNode
} = dataStructureTyped;

生动示例

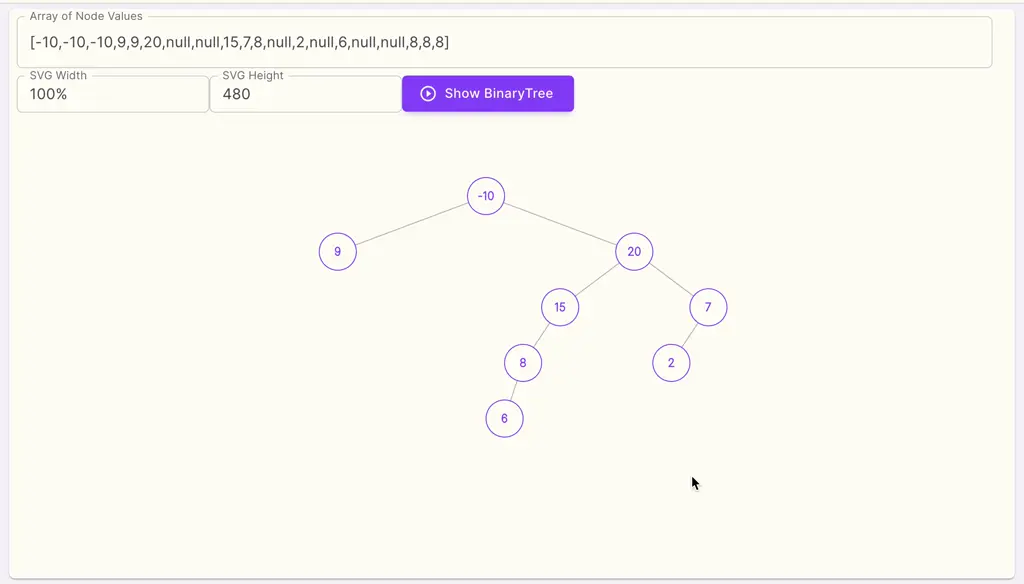
Binary Tree（二叉树）

试一下，或者你可以使用我们的可视化工具运行自己的代码 visual tool

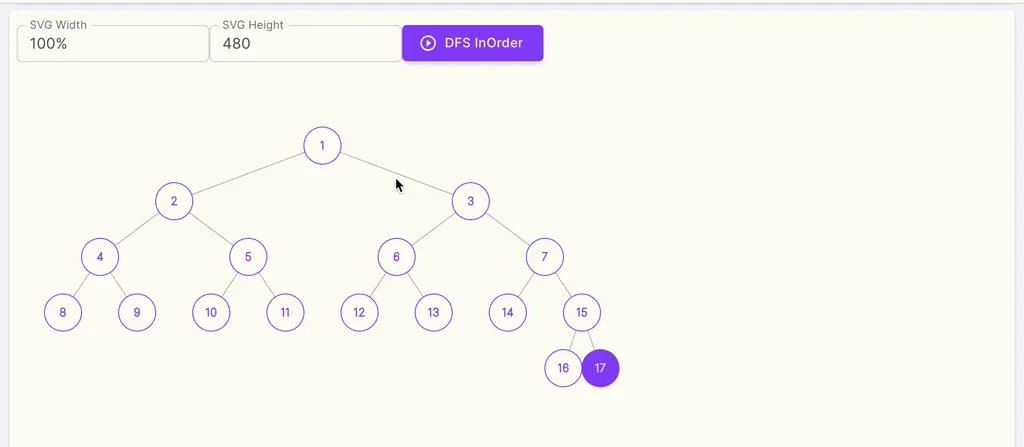
Binary Tree DFS （二叉搜索树深度遍历）

试一下

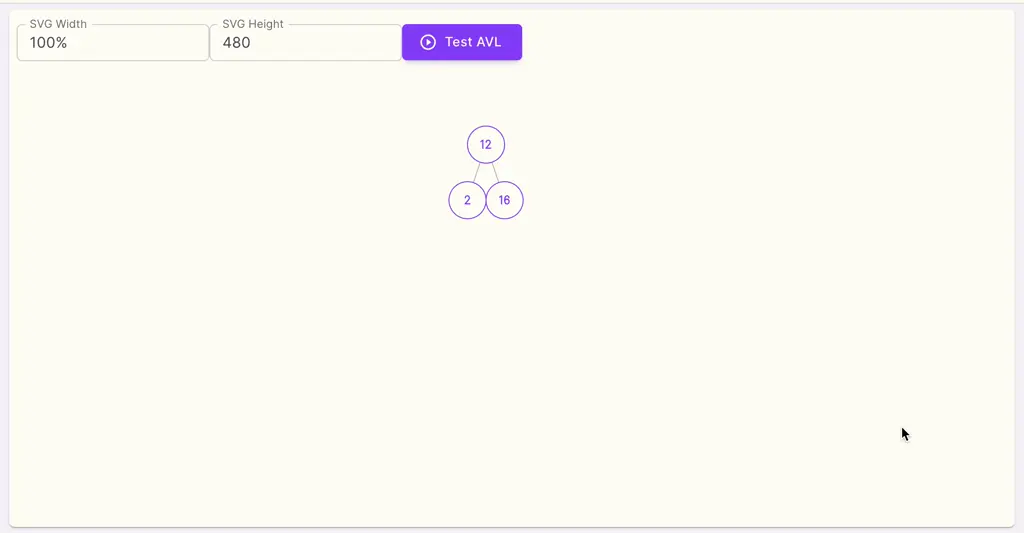
AVL Tree（AVL树）

试一下

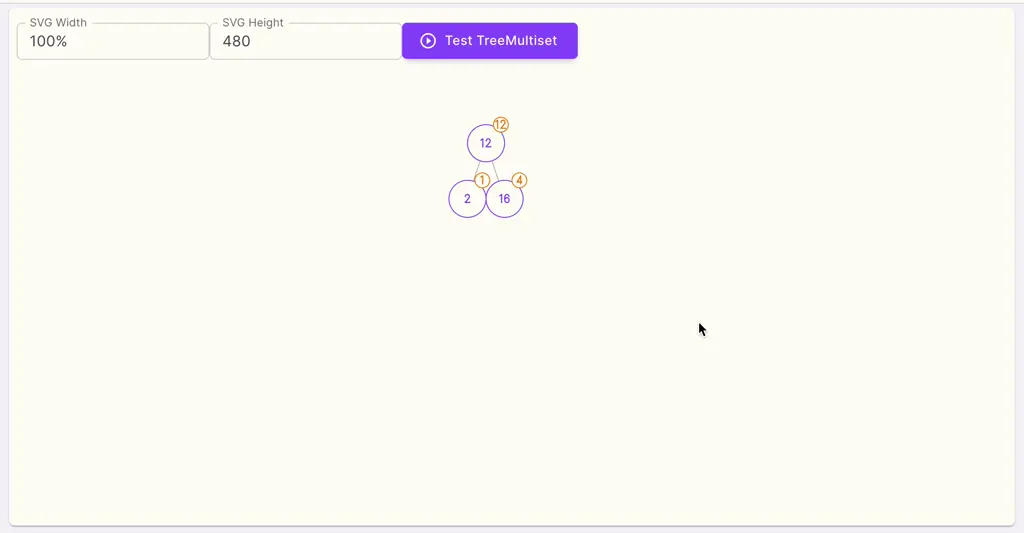
Tree Multi Map

试一下

Matrix

试一下

有向图

试一下

地图

试一下

代码片段

红黑树 代码示例

TS

import {RedBlackTree} from 'data-structure-typed';

const rbTree = new RedBlackTree<number>();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced();    // true
rbTree.delete(10);
rbTree.isAVLBalanced();    // true
rbTree.print()
//         ___6________
//        /            \
//      ___4_       ___11________
//     /     \     /             \
//    _2_    5    _8_       ____14__
//   /   \       /   \     /        \
//   1   3       7   9    12__     15__
//                            \        \
//                           13       16

JS

import {RedBlackTree} from 'data-structure-typed';

const rbTree = new RedBlackTree();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced();    // true
rbTree.delete(10);
rbTree.isAVLBalanced();    // true
rbTree.print()
//         ___6________
//        /            \
//      ___4_       ___11________
//     /     \     /             \
//    _2_    5    _8_       ____14__
//   /   \       /   \     /        \
//   1   3       7   9    12__     15__
//                            \        \
//                           13       16

二叉搜索树 (BST) 代码示例

import {BST, BSTNode} from 'data-structure-typed';

const bst = new BST<number>();
bst.add(11);
bst.add(3);
bst.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5]);
bst.size === 16;                // true
bst.has(6);                     // true
const node6 = bst.getNode(6);   // BSTNode
bst.getHeight(6) === 2;         // true
bst.getHeight() === 5;          // true
bst.getDepth(6) === 3;          // true

bst.getLeftMost()?.key === 1;   // true

bst.delete(6);
bst.get(6);                     // undefined
bst.isAVLBalanced();            // true
bst.bfs()[0] === 11;            // true
bst.print()
//       ______________11_____           
//      /                     \          
//   ___3_______            _13_____
//  /           \          /        \    
//  1_     _____8____     12      _15__
//    \   /          \           /     \ 
//    2   4_       _10          14    16
//          \     /                      
//          5_    9
//            \                          
//            7

const objBST = new BST<number, {height: number, age: number}>();

objBST.add(11, { "name": "Pablo", "age": 15 });
objBST.add(3, { "name": "Kirk", "age": 1 });

objBST.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5], [
    { "name": "Alice", "age": 15 },
    { "name": "Bob", "age": 1 },
    { "name": "Charlie", "age": 8 },
    { "name": "David", "age": 13 },
    { "name": "Emma", "age": 16 },
    { "name": "Frank", "age": 2 },
    { "name": "Grace", "age": 6 },
    { "name": "Hannah", "age": 9 },
    { "name": "Isaac", "age": 12 },
    { "name": "Jack", "age": 14 },
    { "name": "Katie", "age": 4 },
    { "name": "Liam", "age": 7 },
    { "name": "Mia", "age": 10 },
    { "name": "Noah", "age": 5 }
  ]
);

objBST.delete(11);

AVL树 代码示例

import {AVLTree} from 'data-structure-typed';

const avlTree = new AVLTree<number>();
avlTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
avlTree.isAVLBalanced();    // true
avlTree.delete(10);
avlTree.isAVLBalanced();    // true

有向图代码示例

import {DirectedGraph} from 'data-structure-typed';

const graph = new DirectedGraph<string>();

graph.addVertex('A');
graph.addVertex('B');

graph.hasVertex('A');       // true
graph.hasVertex('B');       // true
graph.hasVertex('C');       // false

graph.addEdge('A', 'B');
graph.hasEdge('A', 'B');    // true
graph.hasEdge('B', 'A');    // false

graph.deleteEdgeSrcToDest('A', 'B');
graph.hasEdge('A', 'B');    // false

graph.addVertex('C');

graph.addEdge('A', 'B');
graph.addEdge('B', 'C');

const topologicalOrderKeys = graph.topologicalSort(); // ['A', 'B', 'C']

无向图代码示例

import {UndirectedGraph} from 'data-structure-typed';

const graph = new UndirectedGraph<string>();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.deleteVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'D');

const dijkstraResult = graph.dijkstra('A');
Array.from(dijkstraResult?.seen ?? []).map(vertex => vertex.key) // ['A', 'B', 'D']

不同数据结构之间互相转换

const orgArr = [6, 1, 2, 7, 5, 3, 4, 9, 8];
const orgStrArr = ["trie", "trial", "trick", "trip", "tree", "trend", "triangle", "track", "trace", "transmit"];
const entries = [[6, 6], [1, 1], [2, 2], [7, 7], [5, 5], [3, 3], [4, 4], [9, 9], [8, 8]];

const queue = new Queue(orgArr);
queue.print();      
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const deque = new Deque(orgArr);
deque.print();      
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const sList = new SinglyLinkedList(orgArr);
sList.print();      
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const dList = new DoublyLinkedList(orgArr);
dList.print();      
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const stack = new Stack(orgArr);
stack.print();      
// [6, 1, 2, 7, 5, 3, 4, 9, 8]

const minHeap = new MinHeap(orgArr);
minHeap.print();    
// [1, 5, 2, 7, 6, 3, 4, 9, 8]

const maxPQ = new MaxPriorityQueue(orgArr);
maxPQ.print();      
// [9, 8, 4, 7, 5, 2, 3, 1, 6]

const biTree = new BinaryTree(entries);
biTree.print();
//         ___6___
//        /       \
//     ___1_     _2_
//    /     \   /   \
//   _7_    5   3   4
//  /   \
//  9   8

const bst = new BST(entries);
bst.print();
//     _____5___
//    /         \
//   _2_       _7_
//  /   \     /   \
//  1   3_    6   8_
//        \         \
//        4         9


const rbTree = new RedBlackTree(entries);
rbTree.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9


const avl = new AVLTree(entries);
avl.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const treeMulti = new TreeMultiMap(entries);
treeMulti.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const hm = new HashMap(entries);
hm.print()    
// [[6, 6], [1, 1], [2, 2], [7, 7], [5, 5], [3, 3], [4, 4], [9, 9], [8, 8]]

const rbTreeH = new RedBlackTree(hm);
rbTreeH.print();
//     ___4___
//    /       \
//   _2_     _6___
//  /   \   /     \
//  1   3   5    _8_
//              /   \
//              7   9

const pq = new MinPriorityQueue(orgArr);
pq.print();   
// [1, 5, 2, 7, 6, 3, 4, 9, 8]

const bst1 = new BST(pq);
bst1.print();
//     _____5___
//    /         \
//   _2_       _7_
//  /   \     /   \
//  1   3_    6   8_
//        \         \
//        4         9

const dq1 = new Deque(orgArr);
dq1.print();    
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const rbTree1 = new RedBlackTree(dq1);
rbTree1.print();
//    _____5___
//   /         \
//  _2___     _7___
// /     \   /     \
// 1    _4   6    _9
//      /         /
//      3         8


const trie2 = new Trie(orgStrArr);
trie2.print();    
// ['trie', 'trial', 'triangle', 'trick', 'trip', 'tree', 'trend', 'track', 'trace', 'transmit']
const heap2 = new Heap(trie2, { comparator: (a, b) => Number(a) - Number(b) });
heap2.print();    
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const dq2 = new Deque(heap2);
dq2.print();      
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const entries2 = dq2.map((el, i) => [i, el]);
const avl2 = new AVLTree(entries2);
avl2.print();
//     ___3_______
//    /           \
//   _1_       ___7_
//  /   \     /     \
//  0   2    _5_    8_
//          /   \     \
//          4   6     9

API 文档 & 演示

API 文档

在线演示

演示项目代码仓库

包含的数据结构

Data Structure	Unit Test	Performance Test	API Docs
Binary Tree			View
Binary Search Tree (BST)			View
AVL Tree			View
Red Black Tree			View
Tree Multimap			View
Heap			View
Priority Queue			View
Max Priority Queue			View
Min Priority Queue			View
Trie			View
Graph			View
Directed Graph			View
Undirected Graph			View
Queue			View
Deque			View
Hash Map			View
Linked List			View
Singly Linked List			View
Doubly Linked List			View
Stack			View
Segment Tree			View
Binary Indexed Tree			View

不同编程语言中的数据结构对应关系

Data Structure Typed	C++ STL	java.util	Python collections
Heap<E>	priority_queue<T>	PriorityQueue<E>	heapq
Deque<E>	deque<T>	ArrayDeque<E>	deque
Queue<E>	queue<T>	Queue<E>	-
HashMap<K, V>	unordered_map<K, V>	HashMap<K, V>	defaultdict
DoublyLinkedList<E>	list<T>	LinkedList<E>	-
SinglyLinkedList<E>	-	-	-
BinaryTree<K, V>	-	-	-
BST<K, V>	-	-	-
RedBlackTree<E>	set<T>	TreeSet<E>	-
RedBlackTree<K, V>	map<K, V>	TreeMap<K, V>	-
TreeMultiMap<K, V>	multimap<K, V>	-	-
TreeMultiMap<E>	multiset<T>	-	-
Trie	-	-	-
DirectedGraph<V, E>	-	-	-
UndirectedGraph<V, E>	-	-	-
PriorityQueue<E>	priority_queue<T>	PriorityQueue<E>	-
Array<E>	vector<T>	ArrayList<E>	list
Stack<E>	stack<T>	Stack<E>	-
HashMap<E>	unordered_set<T>	HashSet<E>	set
-	unordered_multiset	-	Counter
LinkedHashMap<K, V>	-	LinkedHashMap<K, V>	OrderedDict
-	unordered_multimap<K, V>	-	-
-	bitset<N>	-	-

内建的经典算法

算法	功能描述	迭代类型
二叉树深度优先搜索(DFS)	以深度优先的方式遍历二叉树，从根节点开始，首先访问左子树，然后是右子树，使用递归。	递归 + 迭代
二叉树广度优先搜索(BFS)	以广度优先的方式遍历二叉树，从根节点开始，逐层从左到右访问节点。	迭代
图的深度优先搜索	以深度优先的方式遍历图，从给定节点开始，尽可能深地沿一条路径探索，然后回溯以探索其他路径。用于寻找连通分量、路径等。	递归 + 迭代
二叉树Morris遍历	Morris遍历是一种中序遍历二叉树的算法，空间复杂度为O(1)。它允许在没有额外栈或递归的情况下遍历树。	迭代
图的广度优先搜索	以广度优先的方式遍历图，从给定节点开始，首先访问与起始节点直接相连的节点，然后逐层扩展。用于寻找最短路径等。	递归 + 迭代
图的Tarjan算法	在图中找到强连通分量，通常使用深度优先搜索实现。	递归
图的Bellman-Ford算法	从单一源点找到最短路径，可以处理负权边	迭代
图的Dijkstra算法	从单一源点找到最短路径，不能处理负权边	迭代
图的Floyd-Warshall算法	找到所有节点对之间的最短路径	迭代
图的getCycles	在图中找到所有循环或检测循环的存在。	递归
图的getCutVertices	在图中找到切点，这些是移除后会增加图中连通分量数量的节点。	递归
图的getSCCs	在图中找到强连通分量，这些是任意两个节点都可以相互到达的子图。	递归
图的getBridges	在图中找到桥，这些是移除后会增加图中连通分量数量的边。	递归
图的拓扑排序	对有向无环图(DAG)进行拓扑排序，以找到节点的线性顺序，使得所有有向边都从较早的节点指向较晚的节点。	递归

软件工程标准

严格尊重计算机科学理论和软件开发规范，我们的LinkedList就是传统意义的LinkedList数据结构，而不是用Deque去代替以便标榜性能测试数据。当然我们也同时实现了基于动态数组的Deque。

原则	描述
实用性	遵循ES6和ESNext标准，提供统一且考虑周到的可选参数，简化方法名称。
可扩展性	遵循OOP（面向对象编程）原则，允许所有数据结构继承。
模块化	包括数据结构模块化和独立的NPM包。
效率	所有方法都提供时间和空间复杂度，可与原生JS性能相媲美。
可维护性	遵循开源社区开发标准，完整文档，持续集成，并遵循TDD（测试驱动开发）模式。
可测试性	自动化和定制单元测试、性能测试和集成测试。
可移植性	计划移植到Java、Python和C++，目前已完成80%。
可复用性	完全解耦，最小化副作用，遵循OOP。
安全性	精心设计的成员变量和方法的安全性。读写分离。数据结构软件不需要考虑其他安全方面。
可扩展性	数据结构软件不涉及负载问题。

基准测试

avl-tree

test name	time taken (ms)	executions per sec	sample deviation
10,000 add randomly	72.48	13.80	0.03
10,000 add & delete randomly	144.14	6.94	0.03
10,000 addMany	69.71	14.35	0.02
10,000 get	54.21	18.45	0.01

binary-tree

test name	time taken (ms)	executions per sec	sample deviation
1,000 add randomly	15.84	63.14	0.00
1,000 add & delete randomly	24.62	40.62	0.00
1,000 addMany	17.85	56.01	0.00
1,000 get	20.83	48.00	0.00
1,000 has	20.78	48.13	0.00
1,000 dfs	186.06	5.37	0.02
1,000 bfs	66.58	15.02	0.02
1,000 morris	298.23	3.35	0.02

bst

test name	time taken (ms)	executions per sec	sample deviation
10,000 add randomly	55.04	18.17	0.01
10,000 add & delete randomly	129.85	7.70	0.01
10,000 addMany	50.40	19.84	0.01
10,000 get	63.39	15.78	0.01

rb-tree

test name	time taken (ms)	executions per sec	sample deviation
100,000 add	113.25	8.83	0.02
100,000 add & delete randomly	305.28	3.28	0.03
100,000 getNode	73.20	13.66	0.03
100,000 add & iterator	159.80	6.26	0.06

comparison

test name	time taken (ms)	executions per sec	sample deviation
SRC PQ 10,000 add	0.17	5872.02	4.08e-5
CJS PQ 10,000 add	0.20	4961.22	1.14e-4
MJS PQ 10,000 add	0.74	1351.47	2.98e-4
SRC PQ 10,000 add & pop	4.62	216.49	0.00
CJS PQ 10,000 add & pop	4.36	229.40	0.00
MJS PQ 10,000 add & pop	3.92	255.23	0.00

directed-graph

test name	time taken (ms)	executions per sec	sample deviation
1,000 addVertex	0.12	8557.70	2.46e-5
1,000 addEdge	7.37	135.70	0.00
1,000 getVertex	0.05	1.91e+4	1.12e-5
1,000 getEdge	22.75	43.96	0.00
tarjan	196.98	5.08	0.01
tarjan all	217.25	4.60	0.03
topologicalSort	177.30	5.64	0.02

hash-map

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 set	153.74	6.50	0.07
1,000,000 Map set	330.02	3.03	0.16
1,000,000 Set add	258.64	3.87	0.06
1,000,000 set & get	138.80	7.20	0.06
1,000,000 Map set & get	352.63	2.84	0.05
1,000,000 Set add & has	217.97	4.59	0.02
1,000,000 ObjKey set & get	414.87	2.41	0.06
1,000,000 Map ObjKey set & get	389.17	2.57	0.07
1,000,000 Set ObjKey add & has	352.67	2.84	0.03

heap

test name	time taken (ms)	executions per sec	sample deviation
100,000 add & pop	90.67	11.03	0.02
100,000 add & dfs	40.30	24.81	0.01
10,000 fib add & pop	414.94	2.41	0.02

doubly-linked-list

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	290.62	3.44	0.10
1,000,000 unshift	253.88	3.94	0.10
1,000,000 unshift & shift	259.65	3.85	0.14
1,000,000 addBefore	463.16	2.16	0.10

singly-linked-list

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push & shift	250.27	4.00	0.08
10,000 push & pop	261.13	3.83	0.03
10,000 addBefore	282.46	3.54	0.02

max-priority-queue

test name	time taken (ms)	executions per sec	sample deviation
10,000 refill & poll	10.49	95.29	0.00

priority-queue

test name	time taken (ms)	executions per sec	sample deviation
100,000 add & pop	110.63	9.04	0.01

deque

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	15.89	62.92	0.00
1,000,000 push & pop	26.45	37.81	0.01
1,000,000 push & shift	27.52	36.34	0.00
1,000,000 unshift & shift	28.82	34.70	0.01

queue

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	51.21	19.53	0.02
1,000,000 push & shift	105.56	9.47	0.05

stack

test name	time taken (ms)	executions per sec	sample deviation
1,000,000 push	43.57	22.95	0.01
1,000,000 push & pop	55.18	18.12	0.01

trie

test name	time taken (ms)	executions per sec	sample deviation
100,000 push	54.08	18.49	0.01
100,000 getWords	77.77	12.86	0.02