mirror of
https://github.com/zrwusa/data-structure-typed.git
synced 2024-11-09 23:54:04 +00:00
41 KiB
41 KiB
Data Structure Typed
Data Structures of Javascript & TypeScript.
Do you envy C++ with STL (std::), Python with collections, and Java with java.util ? Well, no need to envy anymore! JavaScript and TypeScript now have data-structure-typed.
Now you can use this in Node.js and browser environments
CommonJS:require export.modules =
ESModule: import export
Typescript: import export
UMD: var Deque = dataStructureTyped.Deque
Installation and Usage
npm
npm i data-structure-typed --save
yarn
yarn add data-structure-typed
import {
BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultimap,
DirectedVertex, AVLTreeNode
} from 'data-structure-typed';
CDN
Copy the line below into the head tag in an HTML document.
development
<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.js'></script>
production
<script src='https://cdn.jsdelivr.net/npm/data-structure-typed/dist/umd/data-structure-typed.min.js'></script>
Copy the code below into the script tag of your HTML, and you're good to go with your development.
const {Heap} = dataStructureTyped;
const {
BinaryTree, Graph, Queue, Stack, PriorityQueue, BST, Trie, DoublyLinkedList,
AVLTree, MinHeap, SinglyLinkedList, DirectedGraph, TreeMultimap,
DirectedVertex, AVLTreeNode
} = dataStructureTyped;
Vivid Examples
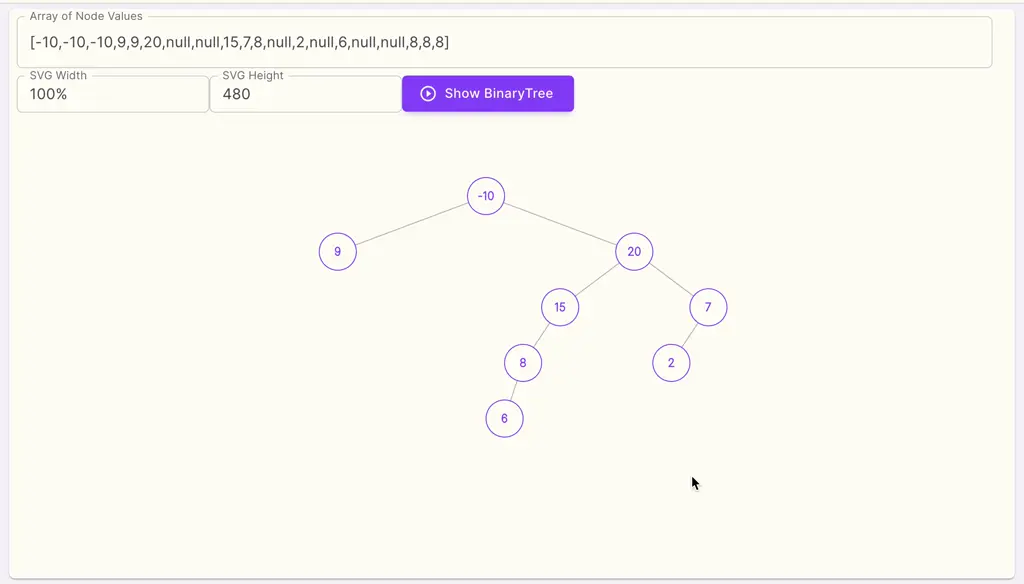
Binary Tree
Try it out, or you can run your own code using our visual tool
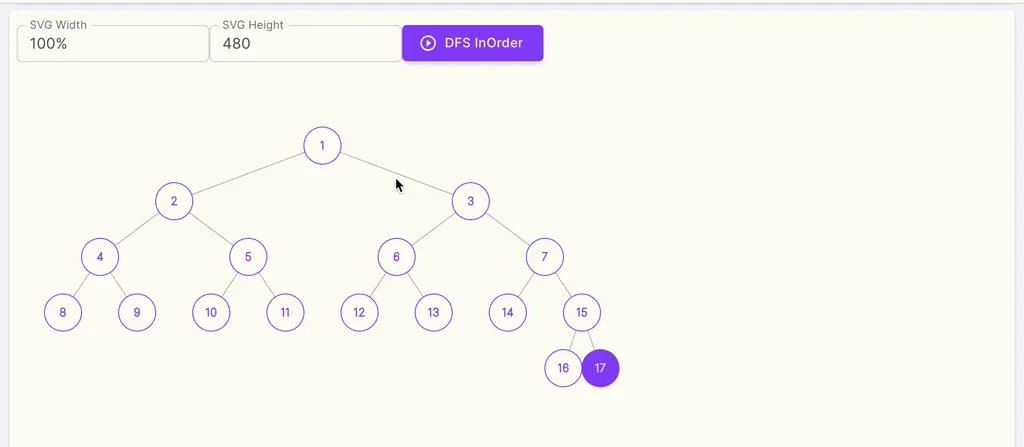
Binary Tree DFS
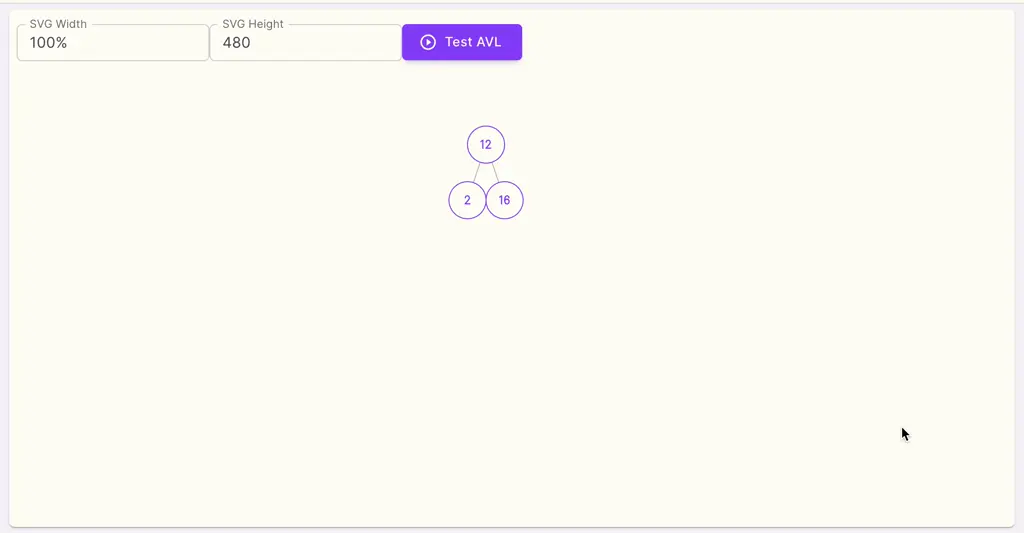
AVL Tree
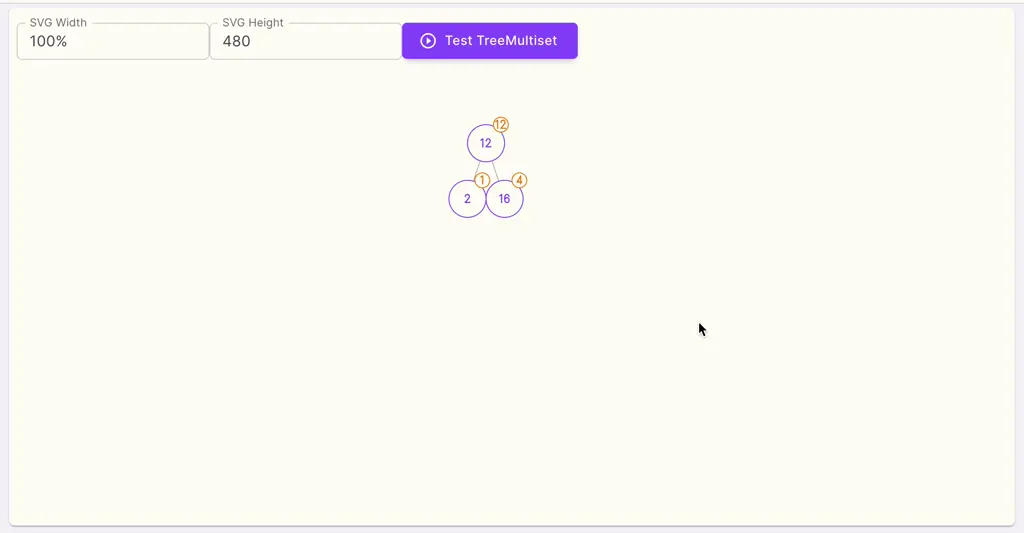
Tree Multi Map
Matrix
Directed Graph
Map Graph
Code Snippets
Binary Search Tree (BST) snippet
TS
import {BST, BSTNode} from 'data-structure-typed';
const bst = new BST();
bst.add(11);
bst.add(3);
bst.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5]);
bst.size === 16; // true
bst.has(6); // true
const node6 = bst.getNode(6); // BSTNode
bst.getHeight(6) === 2; // true
bst.getHeight() === 5; // true
bst.getDepth(6) === 3; // true
bst.getLeftMost()?.key === 1; // true
bst.delete(6);
bst.get(6); // undefined
bst.isAVLBalanced(); // true
bst.bfs()[0] === 11; // true
bst.print()
// ______________11_____
// / \
// ___3_______ _13_____
// / \ / \
// 1_ _____8____ 12 _15__
// \ / \ / \
// 2 4_ _10 14 16
// \ /
// 5_ 9
// \
// 7
const objBST = new BST<{height: number, age: number}>();
objBST.add(11, { "name": "Pablo", "age": 15 });
objBST.add(3, { "name": "Kirk", "age": 1 });
objBST.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5], [
{ "name": "Alice", "age": 15 },
{ "name": "Bob", "age": 1 },
{ "name": "Charlie", "age": 8 },
{ "name": "David", "age": 13 },
{ "name": "Emma", "age": 16 },
{ "name": "Frank", "age": 2 },
{ "name": "Grace", "age": 6 },
{ "name": "Hannah", "age": 9 },
{ "name": "Isaac", "age": 12 },
{ "name": "Jack", "age": 14 },
{ "name": "Katie", "age": 4 },
{ "name": "Liam", "age": 7 },
{ "name": "Mia", "age": 10 },
{ "name": "Noah", "age": 5 }
]
);
objBST.delete(11);
JS
const {BST, BSTNode} = require('data-structure-typed');
const bst = new BST();
bst.add(11);
bst.add(3);
bst.addMany([15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5]);
bst.size === 16; // true
bst.has(6); // true
const node6 = bst.getNode(6);
bst.getHeight(6) === 2; // true
bst.getHeight() === 5; // true
bst.getDepth(6) === 3; // true
const leftMost = bst.getLeftMost();
leftMost?.key === 1; // true
bst.delete(6);
bst.get(6); // undefined
bst.isAVLBalanced(); // true or false
const bfsIDs = bst.bfs();
bfsIDs[0] === 11; // true
AVLTree snippet
import {AVLTree} from 'data-structure-typed';
const avlTree = new AVLTree();
avlTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
avlTree.isAVLBalanced(); // true
avlTree.delete(10);
avlTree.isAVLBalanced(); // true
RedBlackTree snippet
import {RedBlackTree} from 'data-structure-typed';
const rbTree = new RedBlackTree();
rbTree.addMany([11, 3, 15, 1, 8, 13, 16, 2, 6, 9, 12, 14, 4, 7, 10, 5])
rbTree.isAVLBalanced(); // true
rbTree.delete(10);
rbTree.isAVLBalanced(); // true
rbTree.print()
// ___6________
// / \
// ___4_ ___11________
// / \ / \
// _2_ 5 _8_ ____14__
// / \ / \ / \
// 1 3 7 9 12__ 15__
// \ \
// 13 16
Directed Graph simple snippet
import {DirectedGraph} from 'data-structure-typed';
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.hasVertex('A'); // true
graph.hasVertex('B'); // true
graph.hasVertex('C'); // false
graph.addEdge('A', 'B');
graph.hasEdge('A', 'B'); // true
graph.hasEdge('B', 'A'); // false
graph.deleteEdgeSrcToDest('A', 'B');
graph.hasEdge('A', 'B'); // false
graph.addVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'C');
const topologicalOrderKeys = graph.topologicalSort(); // ['A', 'B', 'C']
Undirected Graph snippet
import {UndirectedGraph} from 'data-structure-typed';
const graph = new UndirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.deleteVertex('C');
graph.addEdge('A', 'B');
graph.addEdge('B', 'D');
const dijkstraResult = graph.dijkstra('A');
Array.from(dijkstraResult?.seen ?? []).map(vertex => vertex.key) // ['A', 'B', 'D']
Free conversion between data structures.
const orgArr = [6, 1, 2, 7, 5, 3, 4, 9, 8];
const orgStrArr = ["trie", "trial", "trick", "trip", "tree", "trend", "triangle", "track", "trace", "transmit"];
const entries = [[6, 6], [1, 1], [2, 2], [7, 7], [5, 5], [3, 3], [4, 4], [9, 9], [8, 8]];
const queue = new Queue(orgArr);
queue.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const deque = new Deque(orgArr);
deque.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const sList = new SinglyLinkedList(orgArr);
sList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const dList = new DoublyLinkedList(orgArr);
dList.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const stack = new Stack(orgArr);
stack.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const minHeap = new MinHeap(orgArr);
minHeap.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]
const maxPQ = new MaxPriorityQueue(orgArr);
maxPQ.print();
// [9, 8, 4, 7, 5, 2, 3, 1, 6]
const biTree = new BinaryTree(entries);
biTree.print();
// ___6___
// / \
// ___1_ _2_
// / \ / \
// _7_ 5 3 4
// / \
// 9 8
const bst = new BST(entries);
bst.print();
// _____5___
// / \
// _2_ _7_
// / \ / \
// 1 3_ 6 8_
// \ \
// 4 9
const rbTree = new RedBlackTree(entries);
rbTree.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const avl = new AVLTree(entries);
avl.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const treeMulti = new TreeMultimap(entries);
treeMulti.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const hm = new HashMap(entries);
hm.print()
// [[6, 6], [1, 1], [2, 2], [7, 7], [5, 5], [3, 3], [4, 4], [9, 9], [8, 8]]
const rbTreeH = new RedBlackTree(hm);
rbTreeH.print();
// ___4___
// / \
// _2_ _6___
// / \ / \
// 1 3 5 _8_
// / \
// 7 9
const pq = new MinPriorityQueue(orgArr);
pq.print();
// [1, 5, 2, 7, 6, 3, 4, 9, 8]
const bst1 = new BST(pq);
bst1.print();
// _____5___
// / \
// _2_ _7_
// / \ / \
// 1 3_ 6 8_
// \ \
// 4 9
const dq1 = new Deque(orgArr);
dq1.print();
// [6, 1, 2, 7, 5, 3, 4, 9, 8]
const rbTree1 = new RedBlackTree(dq1);
rbTree1.print();
// _____5___
// / \
// _2___ _7___
// / \ / \
// 1 _4 6 _9
// / /
// 3 8
const trie2 = new Trie(orgStrArr);
trie2.print();
// ['trie', 'trial', 'triangle', 'trick', 'trip', 'tree', 'trend', 'track', 'trace', 'transmit']
const heap2 = new Heap(trie2, { comparator: (a, b) => Number(a) - Number(b) });
heap2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const dq2 = new Deque(heap2);
dq2.print();
// ['transmit', 'trace', 'tree', 'trend', 'track', 'trial', 'trip', 'trie', 'trick', 'triangle']
const entries2 = dq2.map((el, i) => [i, el]);
const avl2 = new AVLTree(entries2);
avl2.print();
// ___3_______
// / \
// _1_ ___7_
// / \ / \
// 0 2 _5_ 8_
// / \ \
// 4 6 9
API docs & Examples
Data Structures
| Data Structure | Unit Test | Performance Test | API Docs |
|---|---|---|---|
| Binary Tree |  |
 |
Binary Tree |
| Binary Search Tree (BST) |  |
 |
BST |
| AVL Tree |  |
 |
AVLTree |
| Red Black Tree |  |
 |
RedBlackTree |
| Tree Multiset |  |
 |
TreeMultimap |
| Segment Tree |  |
SegmentTree | |
| Binary Indexed Tree |  |
BinaryIndexedTree | |
| Heap |  |
 |
Heap |
| Priority Queue |  |
 |
PriorityQueue |
| Max Priority Queue |  |
 |
MaxPriorityQueue |
| Min Priority Queue |  |
 |
MinPriorityQueue |
| Trie |  |
 |
Trie |
| Graph |  |
 |
AbstractGraph |
| Directed Graph |  |
 |
DirectedGraph |
| Undirected Graph |  |
 |
UndirectedGraph |
| Queue |  |
 |
Queue |
| Deque |  |
 |
Deque |
| Linked List |  |
 |
SinglyLinkedList |
| Singly Linked List |  |
 |
SinglyLinkedList |
| Doubly Linked List |  |
 |
DoublyLinkedList |
| Stack |  |
 |
Stack |
Standard library data structure comparison
| Data Structure Typed | C++ STL | java.util | Python collections |
|---|---|---|---|
| Heap<E> | priority_queue<T> | PriorityQueue<E> | heapq |
| Deque<E> | deque<T> | ArrayDeque<E> | deque |
| Queue<E> | queue<T> | Queue<E> | - |
| HashMap<K, V> | unordered_map<K, V> | HashMap<K, V> | defaultdict |
| DoublyLinkedList<E> | list<T> | LinkedList<E> | - |
| SinglyLinkedList<E> | - | - | - |
| BinaryTree<K, V> | - | - | - |
| BST<K, V> | - | - | - |
| RedBlackTree<E> | set<T> | TreeSet<E> | - |
| RedBlackTree<K, V> | map<K, V> | TreeMap<K, V> | - |
| TreeMultimap<K, V> | multimap<K, V> | - | - |
| - | multiset<T> | - | - |
| Trie | - | - | - |
| DirectedGraph<V, E> | - | - | - |
| UndirectedGraph<V, E> | - | - | - |
| PriorityQueue<E> | priority_queue<T> | PriorityQueue<E> | - |
| Array<E> | vector<T> | ArrayList<E> | list |
| Stack<E> | stack<T> | Stack<E> | - |
| Set<E> | - | HashSet<E> | set |
| Map<K, V> | - | HashMap<K, V> | dict |
| - | unordered_set<T> | HashSet<E> | - |
| Map<K, V> | - | - | OrderedDict |
| - | unordered_multiset | - | Counter |
| - | - | LinkedHashSet<E> | - |
| HashMap<K, V> | - | LinkedHashMap<K, V> | - |
| - | unordered_multimap<K, V> | - | - |
| - | bitset<N> | - | - |
Benchmark
avl-tree
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 10,000 add randomly | 33.09 | 30.22 | 4.32e-4 |
| 10,000 add & delete randomly | 74.12 | 13.49 | 0.00 |
| 10,000 addMany | 41.71 | 23.97 | 0.00 |
| 10,000 get | 28.37 | 35.25 | 2.37e-4 |
binary-tree
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000 add randomly | 14.50 | 68.96 | 1.33e-4 |
| 1,000 add & delete randomly | 16.20 | 61.72 | 2.03e-4 |
| 1,000 addMany | 10.51 | 95.12 | 8.76e-5 |
| 1,000 get | 18.28 | 54.69 | 1.82e-4 |
| 1,000 dfs | 157.23 | 6.36 | 7.06e-4 |
| 1,000 bfs | 58.06 | 17.22 | 0.01 |
| 1,000 morris | 256.36 | 3.90 | 0.00 |
bst
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 10,000 add randomly | 30.48 | 32.81 | 4.13e-4 |
| 10,000 add & delete randomly | 71.84 | 13.92 | 0.00 |
| 10,000 addMany | 29.54 | 33.85 | 5.25e-4 |
| 10,000 get | 30.53 | 32.75 | 0.01 |
rb-tree
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 100,000 add | 90.89 | 11.00 | 0.00 |
| 100,000 CPT add | 50.65 | 19.74 | 0.00 |
| 100,000 add & delete randomly | 230.08 | 4.35 | 0.02 |
| 100,000 getNode | 38.97 | 25.66 | 5.82e-4 |
| 100,000 add & iterator | 118.32 | 8.45 | 0.01 |
comparison
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| SRC PQ 10,000 add | 0.14 | 6939.33 | 1.74e-6 |
| CJS PQ 10,000 add | 0.15 | 6881.64 | 1.91e-6 |
| MJS PQ 10,000 add | 0.57 | 1745.92 | 1.60e-5 |
| CPT PQ 10,000 add | 0.57 | 1744.71 | 1.01e-5 |
| SRC PQ 10,000 add & pop | 3.51 | 284.93 | 6.79e-4 |
| CJS PQ 10,000 add & pop | 3.42 | 292.55 | 4.04e-5 |
| MJS PQ 10,000 add & pop | 3.41 | 293.38 | 5.11e-5 |
| CPT PQ 10,000 add & pop | 2.09 | 478.76 | 2.28e-5 |
| CPT OM 100,000 add | 43.22 | 23.14 | 0.00 |
| CPT HM 10,000 set | 0.58 | 1721.25 | 1.85e-5 |
| CPT HM 10,000 set & get | 0.68 | 1477.31 | 1.26e-5 |
| CPT LL 1,000,000 unshift | 81.38 | 12.29 | 0.02 |
| CPT PQ 10,000 add & pop | 2.10 | 476.50 | 1.60e-4 |
| CPT DQ 1,000,000 push | 22.51 | 44.42 | 0.00 |
| CPT Q 1,000,000 push | 47.85 | 20.90 | 0.01 |
| CPT ST 1,000,000 push | 42.54 | 23.51 | 0.01 |
| CPT ST 1,000,000 push & pop | 50.08 | 19.97 | 0.00 |
directed-graph
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000 addVertex | 0.11 | 9501.34 | 6.10e-6 |
| 1,000 addEdge | 6.35 | 157.55 | 6.69e-4 |
| 1,000 getVertex | 0.05 | 2.14e+4 | 2.50e-6 |
| 1,000 getEdge | 25.00 | 39.99 | 0.01 |
| tarjan | 219.46 | 4.56 | 0.01 |
| tarjan all | 218.15 | 4.58 | 0.00 |
| topologicalSort | 176.83 | 5.66 | 0.00 |
hash-map
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000,000 set | 254.46 | 3.93 | 0.04 |
| 1,000,000 CPT set | 251.21 | 3.98 | 0.03 |
| 1,000,000 Map set | 211.27 | 4.73 | 0.01 |
| 1,000,000 Set add | 175.15 | 5.71 | 0.02 |
| 1,000,000 set & get | 370.54 | 2.70 | 0.11 |
| 1,000,000 CPT set & get | 283.34 | 3.53 | 0.07 |
| 1,000,000 Map set & get | 287.09 | 3.48 | 0.04 |
| 1,000,000 Set add & has | 190.50 | 5.25 | 0.01 |
| 1,000,000 ObjKey set & get | 880.47 | 1.14 | 0.10 |
| 1,000,000 Map ObjKey set & get | 334.47 | 2.99 | 0.05 |
| 1,000,000 Set ObjKey add & has | 310.12 | 3.22 | 0.06 |
heap
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 100,000 add & pop | 80.13 | 12.48 | 0.00 |
| 100,000 add & dfs | 35.08 | 28.50 | 0.00 |
| 10,000 fib add & pop | 367.84 | 2.72 | 0.01 |
doubly-linked-list
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000,000 push | 237.28 | 4.21 | 0.07 |
| 1,000,000 CPT push | 75.66 | 13.22 | 0.03 |
| 1,000,000 unshift | 226.38 | 4.42 | 0.05 |
| 1,000,000 CPT unshift | 93.34 | 10.71 | 0.07 |
| 1,000,000 unshift & shift | 188.34 | 5.31 | 0.05 |
| 1,000,000 insertBefore | 329.60 | 3.03 | 0.05 |
singly-linked-list
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 10,000 push & pop | 221.32 | 4.52 | 0.01 |
| 10,000 insertBefore | 255.52 | 3.91 | 0.01 |
max-priority-queue
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 10,000 refill & poll | 9.07 | 110.24 | 2.71e-4 |
priority-queue
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 100,000 add & pop | 101.93 | 9.81 | 7.95e-4 |
| 100,000 CPT add & pop | 28.54 | 35.04 | 0.00 |
deque
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000,000 push | 14.43 | 69.29 | 2.36e-4 |
| 1,000,000 CPT push | 25.08 | 39.87 | 0.01 |
| 1,000,000 push & pop | 22.87 | 43.72 | 6.05e-4 |
| 1,000,000 push & shift | 25.28 | 39.55 | 0.01 |
| 1,000,000 unshift & shift | 21.88 | 45.71 | 2.05e-4 |
queue
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000,000 push | 38.49 | 25.98 | 9.08e-4 |
| 1,000,000 CPT push | 43.93 | 22.76 | 0.01 |
| 1,000,000 push & shift | 82.85 | 12.07 | 0.00 |
stack
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 1,000,000 push | 40.19 | 24.88 | 0.01 |
| 1,000,000 CPT push | 39.87 | 25.08 | 0.00 |
| 1,000,000 push & pop | 41.67 | 24.00 | 0.01 |
| 1,000,000 CPT push & pop | 46.65 | 21.44 | 0.00 |
trie
| test name | time taken (ms) | executions per sec | sample deviation |
|---|---|---|---|
| 100,000 push | 43.42 | 23.03 | 7.57e-4 |
| 100,000 getWords | 93.41 | 10.71 | 0.00 |
Built-in classic algorithms
| Algorithm | Function Description | Iteration Type |
|---|---|---|
| Binary Tree DFS | Traverse a binary tree in a depth-first manner, starting from the root node, first visiting the left subtree, and then the right subtree, using recursion. | Recursion + Iteration |
| Binary Tree BFS | Traverse a binary tree in a breadth-first manner, starting from the root node, visiting nodes level by level from left to right. | Iteration |
| Graph DFS | Traverse a graph in a depth-first manner, starting from a given node, exploring along one path as deeply as possible, and backtracking to explore other paths. Used for finding connected components, paths, etc. | Recursion + Iteration |
| Binary Tree Morris | Morris traversal is an in-order traversal algorithm for binary trees with O(1) space complexity. It allows tree traversal without additional stack or recursion. | Iteration |
| Graph BFS | Traverse a graph in a breadth-first manner, starting from a given node, first visiting nodes directly connected to the starting node, and then expanding level by level. Used for finding shortest paths, etc. | Recursion + Iteration |
| Graph Tarjan's Algorithm | Find strongly connected components in a graph, typically implemented using depth-first search. | Recursion |
| Graph Bellman-Ford Algorithm | Finding the shortest paths from a single source, can handle negative weight edges | Iteration |
| Graph Dijkstra's Algorithm | Finding the shortest paths from a single source, cannot handle negative weight edges | Iteration |
| Graph Floyd-Warshall Algorithm | Finding the shortest paths between all pairs of nodes | Iteration |
| Graph getCycles | Find all cycles in a graph or detect the presence of cycles. | Recursion |
| Graph getCutVertexes | Find cut vertices in a graph, which are nodes that, when removed, increase the number of connected components in the graph. | Recursion |
| Graph getSCCs | Find strongly connected components in a graph, which are subgraphs where any two nodes can reach each other. | Recursion |
| Graph getBridges | Find bridges in a graph, which are edges that, when removed, increase the number of connected components in the graph. | Recursion |
| Graph topologicalSort | Perform topological sorting on a directed acyclic graph (DAG) to find a linear order of nodes such that all directed edges go from earlier nodes to later nodes. | Recursion |
Software Engineering Design Standards
| Principle | Description |
|---|---|
| Practicality | Follows ES6 and ESNext standards, offering unified and considerate optional parameters, and simplifies method names. |
| Extensibility | Adheres to OOP (Object-Oriented Programming) principles, allowing inheritance for all data structures. |
| Modularization | Includes data structure modularization and independent NPM packages. |
| Efficiency | All methods provide time and space complexity, comparable to native JS performance. |
| Maintainability | Follows open-source community development standards, complete documentation, continuous integration, and adheres to TDD (Test-Driven Development) patterns. |
| Testability | Automated and customized unit testing, performance testing, and integration testing. |
| Portability | Plans for porting to Java, Python, and C++, currently achieved to 80%. |
| Reusability | Fully decoupled, minimized side effects, and adheres to OOP. |
| Security | Carefully designed security for member variables and methods. Read-write separation. Data structure software does not need to consider other security aspects. |
| Scalability | Data structure software does not involve load issues. |